Linear Regression คือ อะไร

เป็น Supervised Learning Algorithm ที่ใช้ในการ Model และวิเคราะห์ความสัมพันธ์ระหว่าง ตัวแปรอิสระ (Dependent Variable) และ ตัวแปรตาม (Independent Variables)

มีเป้าหมาย คือ หาเส้นตรงที่ Fit กับข้อมูลได้ดีที่สุด ภายในช่วง (Range) ที่พิจารณา

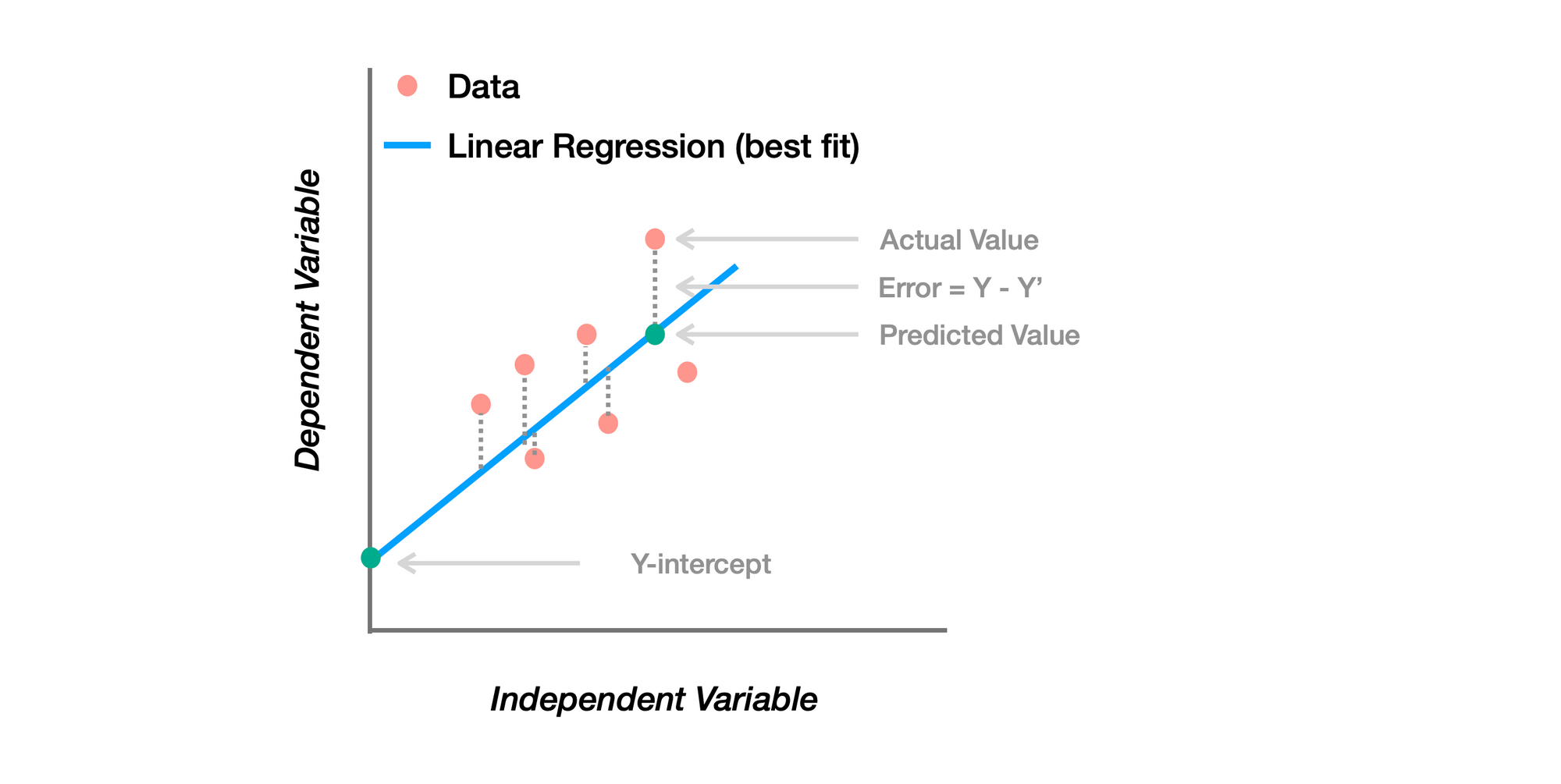
ในทางคณิตศาสตร์ Linear Regression จะใช้ Linear Function 

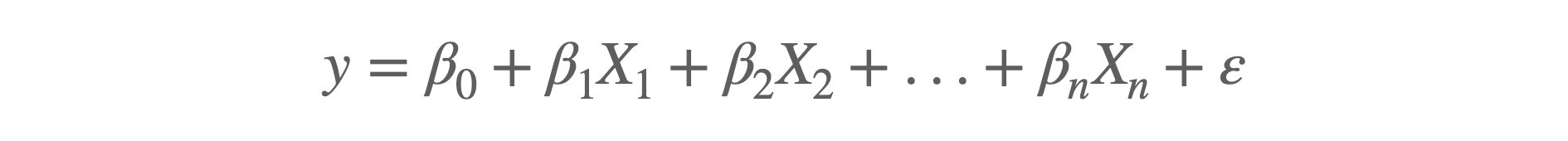
y คือ ตัวแปรอิสระ 

X คือ ตัวแปรตาม

β คือ Regression Coefficients 

ε คือ ค่า Error

Hyper-parameter ของ Linear Regression

เมื่อใช้ Regularization Methods อย่างเช่น Ridge, Lasso Regression การ Fine Tune Hyper-parameter จะมีความสำคัญ

1. Alpha (ɑ) ถูกใช้ใน Ridge และ Lasso Regression เพื่อกำหนดความเข้มข้นในการทำ Regularization ค่าAlpha ที่สูง คือ Regularization ที่มากกว่า และ เป็น Simpler Linear Model สำหรับ ค่า Alpha=0 คือLinear Regression ปกติ
2. Normalization หากกำหนดเป็นค่า True ค่า X จะถูกทำ Normalization ก่อนที่จะทำ Regression โดยการลบกับค่า Mean และหารด้วย L2-norm
3. Fit Intercept เพื่อทำการคำนวณ Intercept สำหรับ Model หากกำหนดเป็น False จะไม่ใช้ Intercept สำหรับ Model
4. Solver คือ Algorithms ที่ใช้ในการ Optimization ได้แก่ auto, svd, cholesky, lsqr, sparse_cg, sag, saga ฯลฯ

Applications

• ทำนายราคาบ้าน
• คาดการณ์ Customer Lifetime Value (CLV)
• คาดการณ์จำนวนเงินที่ลูกค้าจะใช้จ่าย

🟢 ข้อดี 

• ง่ายในการทำความเข้าใจ
• เร็วทั้งในการ Train และ การ Predict
• ทำงานได้ดีกับความสัมพันธ์ที่เป็น Linear

🔴 ข้อเสีย

• สมมติฐานความสัมพันธ์ที่เป็น Linear แต่ Real-world Data ส่วนใหญ่ไม่ใช่
• ไวต่อ Outliers 
• ปัญหาเรื่อง Multicollinearity หาก Dataset มีตัวแปรที่ Correlated กันสูง

ตัวอย่าง Python Code 👨🏻‍💻

# Import Libraries
# ----------
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import mean_squared_error

# Import Boston Dataset
# ----------
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
X = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
y = raw_df.values[1::2, 2]

# Train and Test Splitting
# ----------
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Linear Regression Model
# ----------
linear_model = LinearRegression()
linear_model.fit(X, y)
y_pred = linear_model.predict(X_test)

print (f"Linear Regression MSE: {mean_squared_error(y_test, y_pred)})")

ทดลองใช้ Ridge Regression กับ Hyper-parameter Tuning ที่ค่า Alpha และใช้ Grid Search เพื่อหาค่า Alpha ที่ดีที่สุด

# Ridge Regression with hyperparameter tuning
# Defind the hyperparameters
# ----------
alphas = np.logspace(-6, 6, 13)
parameters = {'alpha':alphas}

ridge = Ridge()
grid_search = GridSearchCV(ridge, parameters, scoring='neg_mean_squared_error', cv=5)

grid_search.fit(X_train, y_train)

# Best hyperparameter setting
# ----------
best_alpha = grid_search.best_params_['alpha']

ridge_regressor = Ridge(alpha=best_alpha)
ridge_regressor.fit(X_train, y_train)
y_pred_ridge = ridge_regressor.predict(X_test)

print (f"Ridge Regression MSE: {mean_squared_error(y_test, y_pred_ridge)})")

******

อ่านเพิ่มเติม Pros & Cons ของ Machine Learning Algorithms ที่นิยมใช้

******

ข้อมูลอ้างอิง - Analytics Vidhya