รู้จักกับ Clustering Algorithms

Clustering เป็น "Unsupervised Learning" มีเป้าหมายเพื่อแบ่งข้อมูลออกเป็นกลุ่ม ตามความคล้ายคลึงกัน

• Clustering Algorithms จำนวนมากถูกพัฒนาขึ้น ในแต่ละ Algorithms จะพิจารณาเฉพาะบางปัจจัยเท่านั้น ได้แก่ ขนาด, รูปร่าง, ความหนาแน่น (Dense), ลำดับชั้น (Hierarchy), การทับซ้อน หรือ ความไม่ต่อเนื่องของ Clusters รวมถึงการหา "ค่าผิดปกติ" หรือ  "Noise" ดังนั้น จึงไม่มี Algorithms สำหรับ Clustering ที่ "แท้จริง"
• Blog นี้จะกล่าวถึง วิธี Clustering ที่สำคัญ และ ข้อดี / ข้อเสีย ของแต่ละวิธี ดังนี้

1) Hierarchical Clustering

2) DBSCAN

3) Partitional Clustering

4) Expectation Maximization (EM) Clustering

5) Non-negative Matrix Factorization (NMF)

1) Hierarchical Clustering

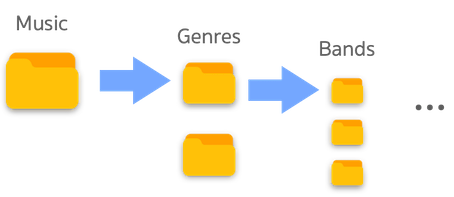
• ที่ Folder Home ของคอมพิวเตอร์ จะมี Folders ย่อยต่าง ๆ เช่น Download, Application, Movies, Music  และ แต่ละ Folders ย่อยเหล่านี้ ก็จะมีรายการ Folders ย่อยลงไปอีก
• Folder Music อาจมี Folder ย่อยของประเภทเพลงที่ต่างกัน ลึกลงไปมี Folders ย่อยของวงดนตรีที่ต่างกัน และ จากนั้นเป็น Folders อัลบั้มที่จัดกลุ่มตามปี เราสามารถเปรียบเทียบ Hierarchical Clustering เหมือน ๆ กับ การจัดเรียง Folders นี้

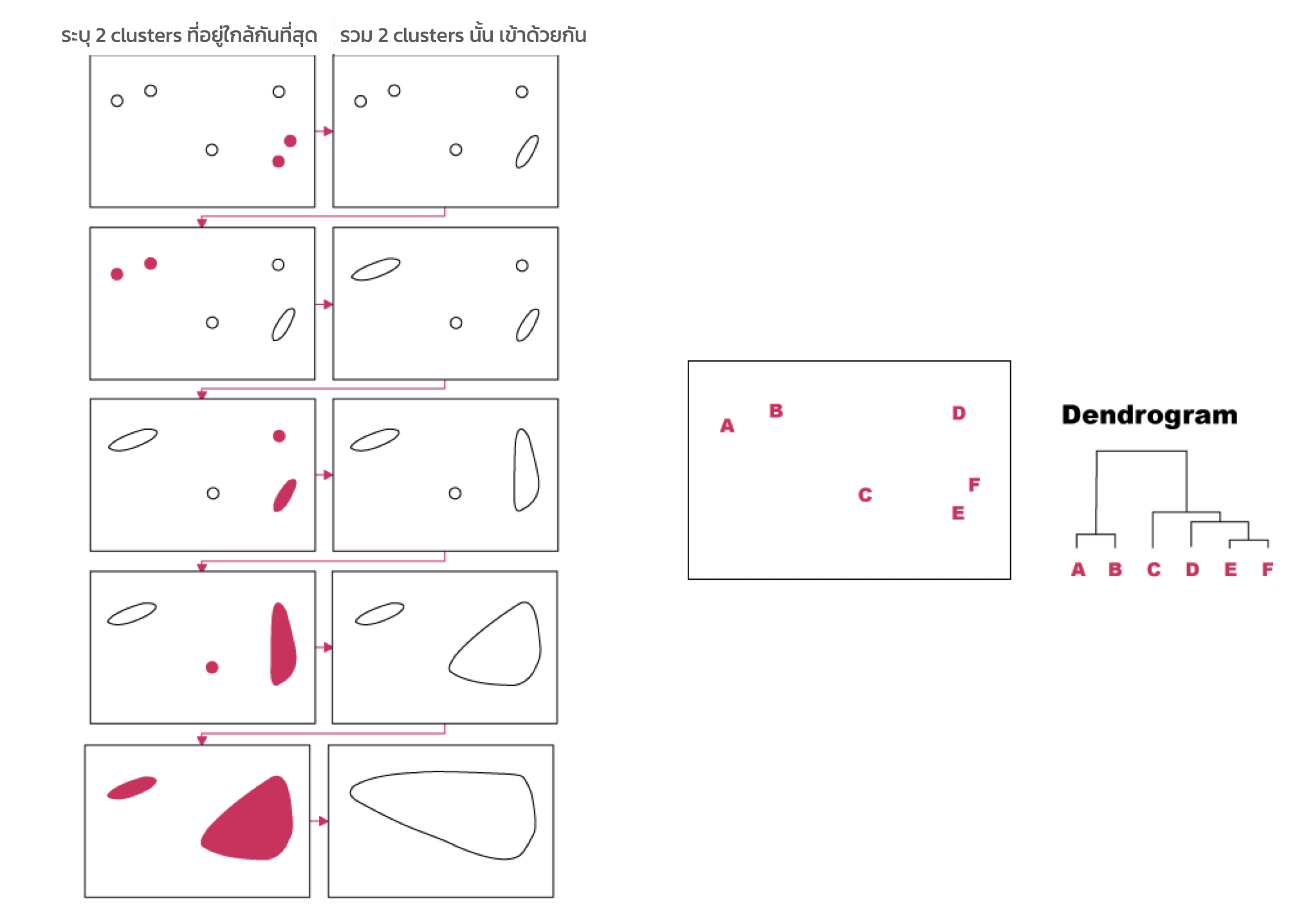
• เป้าหมายของ Hierarchical Clustering คือ การสร้าง Hierarchy ของ Objects ที่คล้ายกัน แผนภาพต้นไม้ (Tree diagram) ที่มี Objects ทั้งหมดอยู่ที่ Root และ แบ่งกลุ่ม Objects  ต่าง ๆ ไปที่ Child branches ถูกเรียกว่า "Dendrogram" มี 2 แนวทาง ที่แตกต่างกัน คือ Agglomerative และ Divisive

Agglomerative (จากล่างขึ้นบน - Bottom up)

ขั้นตอนของ Agglomerative

1. มองแต่ละ Object ในชุดข้อมูลเป็น Cluster ที่แยกกัน
2. ระบุ 2 กลุ่มที่คล้ายกัน
3. รวมเป็น 1 Cluster
4. ทำซ้ำ ข้อ 2 และ 3 จนกระทั่งเหลือเพียง Cluster เดียว

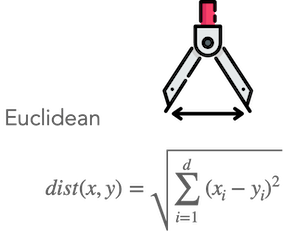
• การวัดความคล้ายกัน ทำได้โดยใช้ "Function ระยะทาง" เช่น Euclidean
• Function ระยะทาง คำนวณจาก 2 จุด หาก "ระยะทางใกล้กัน" แสดงว่า "มีความคล้ายกันมาก"
• Metrics การวัดระยะทางมีหลายแบบ เช่น Manhattan, Chebychev ฯลฯ

เกณฑ์การเชื่อมโยง (Linkage Criteria)

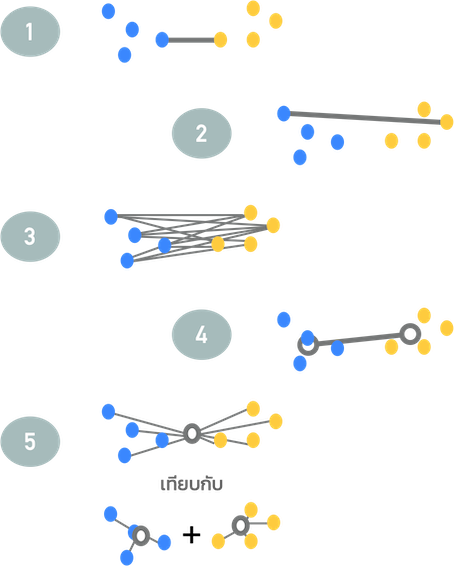
• ในการ Clustering ต้องทราบระยะทางระหว่างกลุ่ม เกณฑ์การเชื่อมโยง (Linkage Criteria) มี 5 ประเภท คือ

1. Single-Linkage: ระยะทาง ระหว่างจุดที่ใกล้สุดใน 2 Clusters
2. Complete-Linkage: ระยะทาง ระหว่างจุดที่ไกลสุดใน 2 Clusters
3. Average-Linkage: ระยะทางเฉลี่ยของจุดทุกคู่ ใน 2 Clusters
4. Centroid-Linkage: ระยะทาง ระหว่างจุด Centroids ของ  2 Clusters
5. Ward’s distance: การวัดความเปลี่ยนแปลง ระยะทางรวมทั้งหมด จากศูนย์กลาง (Centroid) เมื่อกำลังรวม 2 Clusters เข้าด้วยกัน

Divisive (จากบนลงล่าง - Top down)

• ตรงข้ามกับ Agglomerative แทนที่จะรวม Objects ที่คล้ายกันจาก Leaf node แต่ทุก Objects จะเริ่มต้นใน Cluster เดียวที่ Root node และ แยกจุดเหล่านี้ออกเป็น 2 Partitions ซึ่งมีความแตกต่างกันสูงสุด ในวิธีนี้ จะเลือกกลุ่มที่มี ความแปรปรวน (Variance) สูงกว่า เพื่อแยกในแต่ละ Iteration
• การพิจารณาว่า จะแยกกลุ่มเหล่านี้อย่างไร ? ต้องคำนวณระยะทางระหว่าง Objects ทุกคู่ ด้วย Function ระยะทางที่เหมาะสม และ สร้าง Dissimilarity Matrix เพื่อหาคู่ของ Objects ที่ไกลกันที่สุด (แตกต่างกันมากที่สุด) เพื่อให้ได้มาซึ่ง Optimal Split (การแยกที่เหมาะสม)

แม้ว่า Hierarchical Algorithm นั้นง่ายต่อการทำความเข้าใจ และ นำไปใช้ แต่มีข้อด้อย คือ

• Hierarchical  ไม่มีการย้อนกลับ คือ หากมีข้อผิดพลาด ต้องเริ่มกระบวนการใหม่ตั้งแต่ต้น
• หากชุดข้อมูลมีขนาดใหญ่มาก Dendrogram อาจสร้างความสับสน (ยาก ที่จะกำหนดจำนวนของกลุ่มด้วยตา)
• ใช้เวลาในการประมวลผลนานกว่าวิธีอื่น ๆ (อย่างเช่น K-means)

2) DBSCAN

• DBSCAN (Density-Based Spatial Clustering of Applications with Noise) เป็น Algorithm การจัดกลุ่ม (Cluster) ตาม "ความหนาแน่น (Density-based)"
• DBSCAN จะกำหนด "Core และ Border Objects" ส่วนที่เหลือจะพิจารณาเป็น "Noise"
• ในทางทฤษฎี Clustering แบบ Density-based พิจารณา 2 เงื่อนไข คือ

1) Maximality: ในการเลือก Object ใด เข้ามาใน Cluster ค่าความหนาแน่น ต้องมากกว่า Threshold [Density Reachable]

2) Connectivity: Objects ทั้งหมดใน Cluster ต้องเชื่อมต่อ (Connect) กันเชิงพื้นที่ [Density Connected]

• DBSCAN พัฒนาบนพื้นฐานของ .. เซตของ Objects, Function ระยะทาง, ทรงกลมรัศมี Epsilon รอบ Object (เรียกว่า Epsilon-Neighborhood, Eps) และ Minimum Objects ใน Eps (เรียกว่า MinPts)
• สามารถกำหนด ค่าต่าง ๆ  ได้ดังนี้

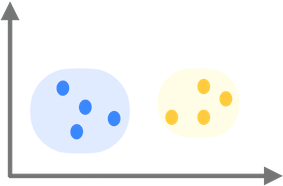
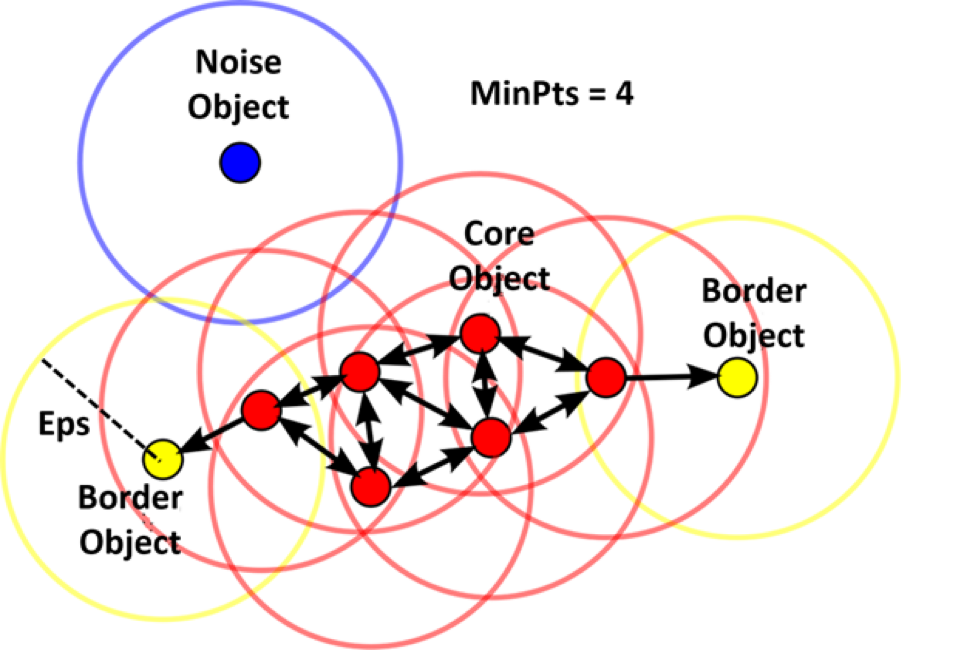
Core Object ถ้าทรงกลมที่มีรัศมี Eps อยู่กึ่งกลางที่ Core Object มันมีจำนวน Objects อย่างน้อย MinPts ในรูป กำหนด MinPts = 4 และ Core Object จะแสดงเป็นสีแดง

Density Reachable Objects จะอยู่ภายใน Eps ของ Core Objects ซึ่งก่อให้เกิด Chain ของ Reachable Objects ในรูปแสดงเป็นสีแดงและสีเหลือง

Border Object ไม่ใช่ Core แต่มี Density Reachable (เข้าถึงได้) จาก Core Objects Border Objects จะแสดงเป็นสีเหลือง

• Connectivity Object พิจารณาที่ Core Objects ความหมายของ Direct Density Reachability คือ ความสัมพันธ์แบบ Symmetry แสดงโดยลูกศรสองด้าน (ดังรูป) สำหรับ General Density Reachability คือ ความสัมพันธ์แบบ Non-symmetry (ไม่มี non-core object ที่เข้าถึงได้) จากรูป Border Object ไม่มี Density Reachable จาก Border Object อื่น
• Noise คือ Object ที่ไม่ได้เป็นของกลุ่มใด ๆ แสดงเป็นสีน้ำเงิน

ข้อดี / ข้อเสีย ของ Density-based

ข้อดีของ Density-based clustering

• ตรวจจับกลุ่มของรูปร่างใด ๆ ก็ได้ (Arbitrary Shapes)
• ทนต่อ Noise
• มีประสิทธิภาพ
• ไม่ต้องกำหนดจำนวนกลุ่ม เป็นพารามิเตอร์ Input ซึ่งแตกต่างจาก Model ที่ใช้ "Partitional Clustering"

ข้อเสียของ Density-based clustering

• DBSCAN ไม่สามารถจัดการกับ Hierarchical Clustering ได้
• มันจะพยายามหา Density ที่แตกต่างกัน ในพื้นที่ต่าง ๆ ของข้อมูล  ไม่สามารถแยก Cluster และ Noise ได้ง่ายนัก เพื่อแก้ไขปัญหานี้ จึงมีวิธีแบบ Hierarchical Density-based Clustering เช่น OPTICS และ HDBSCAN

นอกจากนี้ ยังมีวิธีอื่น ๆ ที่พัฒนาจาก DBSCAN คือ Generalized DBSCAN, GDBSCAN, Rough-DBSCAN

3) Partitional Clustering

• Partitional Clustering จำนวนกลุ่ม K จะถูกกำหนดล่วงหน้า
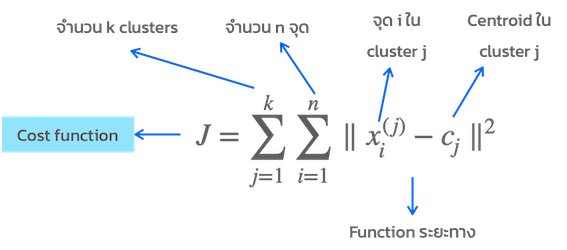
• ดังนั้น ข้อมูลจะถูกแบ่งออกเป็น K กลุ่ม แต่ละ Object จะถูกกำหนดให้อยู่ใน Cluster ที่คล้ายกันมากที่สุด ในขณะที่ Cost Function จะลดลงเรื่อย ๆ ทุกรอบของการคำนวณ
• Partitional Clustering มี 2 วิธีหลัก ๆ คือ K-means, K-medoids

K-means

ขั้นตอนการทำงานของ K-mean

1. เลือกจำนวน K กลุ่ม
2. กำหนด Centroid เริ่มต้น แบบสุ่ม (K กลุ่ม) เป็นตัวแทน Cluster
3. คำนวณระยะทาง / กำหนดแต่ละจุดข้อมูล ให้เป็นสมาชิกของ Centroid ที่ใกล้ที่สุด
4. ในแต่ละ Cluster คำนวณ / Update ค่าเฉลี่ยของ Centroid ใหม่
5. ทำซ้ำข้อ 3 และ 4 เพื่อค้นหา K Centroids ที่ดีที่สุด จนกว่าจะลู่เข้า (Convergence) หรือ ครบจำนวนการวนซ้ำที่กำหนดไว้ล่วงหน้า

Note

• มีกระบวนการ Post-processing ที่เป็นไปได้ เช่น ISODATA กำจัดกลุ่มที่มีขนาดเล็กเกินไป หรือ แบ่งกลุ่มที่ใหญ่เกินไป ให้เล็กลง
• ทั้งนี้ ต้องมีการกำหนดค่า Max/Min ของขนาด Cluster เพิ่มเติม

K-medoids

• ขั้นตอนการทำงานของ K-medoids (หรือ Partitioning Around Medoids, PAM)

1. เลือกจำนวน K กลุ่ม
2. เลือกตัวแทนกลุ่มเริ่มต้น K กลุ่ม เพื่อเป็นตัวแทน Medoids จากชุดข้อมูล
3. เชื่อมโยงแต่ละจุดข้อมูล กับ Medoid ที่ใกล้เคียงที่สุด
4. สลับ "แต่ละ Mediod" กับ "แต่ละจุดข้อมูล" คำนวณ Cost function ทำการ Update ค่า Medoid ใหม่ โดยพิจารณาจาก Cost function ที่ดีที่สุด
5. ทำซ้ำข้อ 3 และ 4 เพื่อค้นหา K medoids ที่ดีที่สุด จนกว่าจะลู่เข้า (Convergence) หรือ ครบจำนวนการวนซ้ำที่กำหนดไว้ล่วงหน้า

Note

• K-medoids เหมาะกับข้อมูล Numerical และ Categorical, ทนทานต่อ Noise และ Outliers มากกว่า K-means
• ข้อเสีย คือ มีการคำนวณเยอะ เพราะต้องคิดทุก ๆ การสลับที่เป็นไปได้ (ในช่วงการคำนวณเพื่อ update medoids)
• มี Algorithm อื่น ๆ ที่ถูกพัฒนาต่อยอดจาก K-medoids เช่น CLARANS

4) Expectation Maximization (EM) Clustering

• เป็น Probabilistic model-based คือ การ Generalization ของ K-means
• ใน K-means เราใช้จุดศูนย์กลางเป็นตัวแทนของ Cluster ใน EM ต้วแทนของ Cluster จะถูกกำหนดโดย Probability Density Function (PDF) ทั่ว ๆ ไป เป็น Guassian Distribution โดย Cluster ถูกแทนด้วย Mean (ค่าเฉลี่ย) และ Covariance matrix ของจุดใน Cluster นั้น Covariance matrix จะแสดงการแพร่ขยายของ Cluster ในทิศทางต่าง ๆ กัน
• EM ทุกจุดจะถูก Soft-assigned โดย Probability Distribution ไม่เหมือน K-means ซึ่งแต่ละจุดข้อมูล จะถูก assigned เพียงแค่ Cluster เดียว (hard assigned)
• สมมติฐานของ EM คือ จุดข้อมูลเกิดขึ้นอย่างอิสระต่อกัน ใน Distribution เดียวกัน ดังนั้น EM จึงใช้ Maximum Likelihood เพื่อ Optimal ในการกำหนดจุดลง Cluster ใดๆ

ข้อดีของ EM เมื่อเทียบกับ K-means

• EM จะให้ข้อมูลมากกว่า เพราะเป็น Soft-assigned
• นอกจากนี้ยังสามารถ Clustering กลุ่มที่ไม่เป็นทรงกลม ซึ่งแตกต่างจาก k-means

ข้อเสียของ EM เมื่อเทียบกับ K-means

• ในการเริ่มต้นจะยากกว่า เพราะต้องกำหนด Parameters หลายตัว ให้กับ Algorithm
• นอกจากนี้ยังทำงานช้ากว่า K-means มาก เนื่องจากต้องมีการวนซ้ำ (Iteration) จำนวนมาก (เพื่อ Optimization)

5) Non-negative Matrix Factorization (NMF)

• คือ Dimensionality Reduction ดูผิวเผิน วิธีการนี้เหมือนจะไม่เกี่ยวกับ Clustering แต่เมื่อพิจารณาอย่างลึกซึ้ง มันสามารถใช้ Clustering ได้
• NMF ถูกใช้ในหลาย Applications เช่น Image Recognition, Recommender System
• Image คือ ตัวอย่างหนึ่งของ Non-negative matrix ค่า Pixel มีค่าระหว่าง 0-255 หรือ Utility matrix ใน Recommendation เป็นอีกตัวอย่างของ Non-negative sparse matrix (ดังตัวอย่าง)

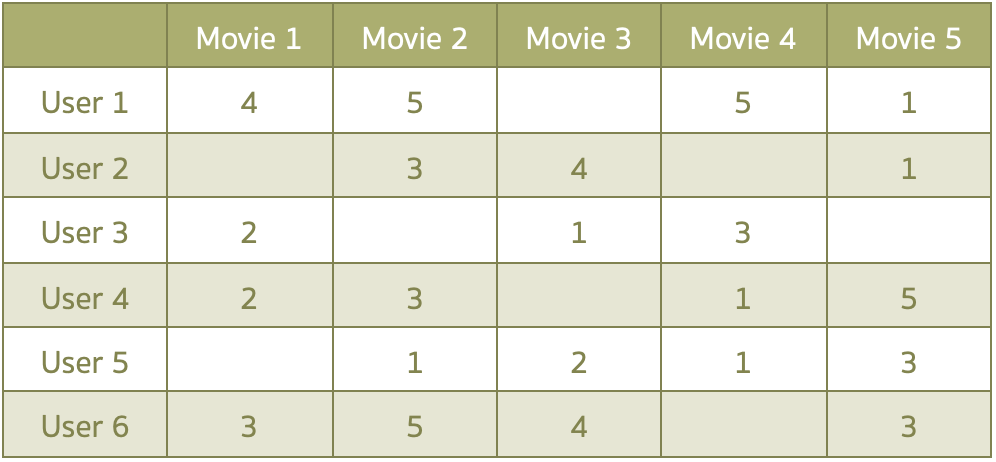
ให้ Data matrix (X) มี m แถว และ n คอลัมน์ เมื่อทุก ๆ ค่าใน X มากกว่าหรือเท่ากับ 0

NMF จะหา 2 matrices ที่เล็กกว่า : W คือ User matrix (Basis) และ H คือ Item matrix (Coefficient)

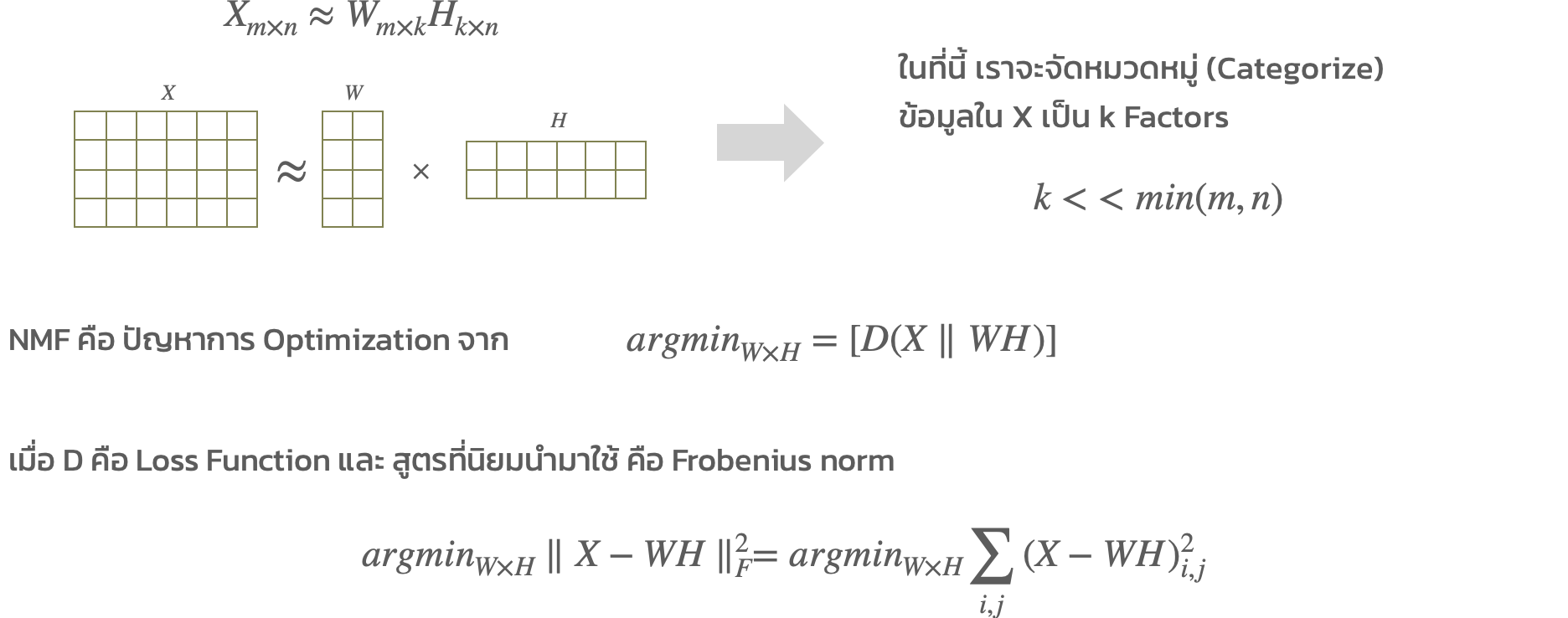
วิธีการที่ใช้แก้ปัญหา NMF จะเป็น Iterative ได้แก่ alternating least squares, multiplicative update, projected gradient descent, active set, optimal gradient, block principal pivoting

ขั้นตอนในการแก้ปัญหา NMF

• โดยทั่วไปขั้นตอนในการแก้ปัญหา NMF มีดังนี้

1. สุ่มค่า Matrix W และ H
2. เปลี่ยนค่าของ W และ H ในแต่ละ iteration เพื่อให้ใกล้เคียงกับ X มากที่สุด

• สำหรับ Alternating Least Squares มีขั้นตอนดังนี้

1. เริ่มต้นค่า W และ H
2. พิจารณาว่า เรารู้ค่าที่ถูกต้องของ W แล้ว จากนั้น พยายาม Minimize ค่าของ H
3. ให้ H คงที่ และ หาค่าของ W
4. ทำซ้ำข้อ 2 และ 3 จนกระทั่ง Convergence

สรุป

เป็น Blog เกี่ยวกับ Clustering Algorithms บางส่วน แต่ยังมีอีกหลาย Algorithms (การนำไปใช้ขึ้นกับปัญหาของเรา) เช่น

• Sub-space Clustering และ Projected Clustering ถูกพัฒนาขึ้น สำหรับกรณีข้อมูล High-dimension
• Semi-supervised Clustering คือ มีการให้เงื่อนไขบางอย่าง (เช่น domain knowledge)
• Constrained K-means clustering
• Probabilistic models for semi-supervised clustering based on Hidden Markov Random Fields
• Cluster ensembles (consensus clustering หรือ multi-view clustering) เป็นวิธีที่รวมหลาย ๆ เทคนิค เพื่อสร้างผลลัพธ์ที่เข้าใจได้มากขึ้น ซึ่งมีทั้ง Model-based และ Data-based ensembles
• การทำ Validation ของ Clustering เป็นเรื่องยาก

หากมี Label สามารถทำการวัดแบบทั่ว ๆ ไป ->โดยใช้ Confusion Matrix, Purity, Entropy, Rand Index

แต่ปกติแล้ว จะไม่มี Label ให้ทำการวัด -> โดยใช้ Compactness ของ Cluster, แต่ละ Cluster แยกกันได้ดีแค่ไหน, ค่าสัมประสิทธิ์ Silhouette เพื่อวัดความเหมือนกันของ Objects ใน Cluster มันเอง เปรียบเทียบกับ Cluster อื่น, ค่า likelihood สำหรับ Probabilistic model-based

• โดยสรุป แต่ละ Algorithm จะให้บางมุมมองของการ Cluster ดังนั้น Algorithms ที่ต่างกัน อาจให้ผลที่แตกต่าง แม้ว่าจะเป็นข้อมูลชุดเดียวกัน มันเป็นการยากมาก ที่จะบอกว่า Algorithm ใด ดีที่สุด ตามที่บอก ในตอนต้นว่า ไม่มีวิธีการสำหรับ Clustering ที่ "แท้จริง"

******

ข้อมูลอ้างอิง - https://medium.com/sfu-big-data/why-so-many-different-clustering-algorithms-2fd94906c668